天津财经大学应用数学硕士研究生培养方案

天津财经大学应用数学硕士研究生培养方案

  二级学科（专业）代码：070104

  所属学科门类名称及代码：数学（07）

  所属一级学科名称及代码：数学（0701）

  所属学院：理工学院

  一、培养目标及基本要求

  本专业硕士研究生的培养目标是培养德、智、体美劳全面发展，具有宽厚的理论知识和应用能力，能适应社会主义现代化建设需要的应用数学方面的高层次专业人才。能较好地利用专业知识为社会主义现代化建设服务，能独立从事应用数学相关的科研、教学或其它实际工作。

  本专业硕士研究生的基本要求是：

  1．努力学习和掌握马克思主义、毛泽东思想和邓小平理论，认真贯彻“三个代表”重要思想，落实科学发展观，习近平新时代中国特色社会主义思想；树立正确的人生观、价值观、世界观；热爱祖国，遵纪守法，品行端正，学风严谨。

  2．掌握本学科的基础理论和专门知识、研究方向的发展现状、趋势和研究前沿。

  3．具有独立地从事科学研究的能力。

  4．熟练掌握一门外语。 2

  二、研究方向

  本学位点主要有三个培养方向：

  1．应用微分方程方向

  本研究方向主要对一些微分方程给出定性的理论结果。

  2．动力学拓扑优化方向

  本研究方向主要研究拓扑优化对偶空间的构建机理并考虑屈曲稳定性的连续体结构动力学模型化技术。

  3．数学建模与系统优化方向

  本研究方向主要以数学为基础，依托我校经济、金融、管理科学等专业优势，寻求准确描述经济系统的运行规律。

  三、学习年限

  本专业硕士研究生学制为3年，最长学习年限为6年。

  四、培养方式

  1．研究生培养实行导师负责制。导师要从每个硕士研究生的具体情况出发，因材施教，严格要求，全面关心硕士研究生的成长。要定期了解硕士研究生的思想、学习和科研状况，及时给予指导与帮助，做到既教书又育人。

  2．政治理论学习与经常性的思想教育相结合。硕士研究生除学习必需的政治理论课以外，还要加强形势、政策、纪律、道德教育，积极参加有益的社会活动和公益劳动等。

  3．硕士研究生的理论课学习，采取课堂讲授、自学和专题研讨相结合的方式进行。教师在教学活动中要充分发挥硕士研究生的主动性和自觉性，激发其深入思考与创新的意3

  识，培养其自我更新知识和调整知识结构的能力，以及独立发现、分析和解决问题的能力。

  五、学分要求

  本专业硕士研究生最低学分要求为43学分，其中，必修课27学分，选修课14学分，其他必修环节2学分。

  六、学术活动与科学研究

  1．学术活动

  在学期间须参加以下学术活动中的至少一项，并在申请答辩前报本学科学术委员会审核：

  （1）参加全国性或国际学术会议1次；

  （2）参加校院组织的学术讲座1次；

  （3）参加校院组织的学术论坛1次。

  2．科学研究

  本专业研究生须具备的科研能力以及应取得的研究成果：

  （1）本专业研究生通过科研训练应全面系统掌握学科前沿研究成果与发展趋势，熟悉本学科的研究方法，具备独立开展科研工作的能力。

  （2）科研成果按学校关于研究生在学期间科研训练与科研成果要求相关规定执行。

  七、毕业（学位）论文

  （一）学位论文基本要求

  要求对所研究的课题有新见解或新成果，并对本学科发4

  展或经济建设、社会进步有一定意义，表明作者在本门学科上掌握坚实的基础理论和系统的专业知识，具有从事科学研究工作或承担专门技术工作的能力。

  （二）论文选题

  1．选题要考虑本学科前沿或对社会发展和国民经济建设有重要意义的课题。

  2．选题应考虑到有一定的先进性和适当的难度，既要有理论分析、又要有实验验证。

  3．导师结合硕士生的特长和兴趣指导选题。

  4．鼓励由研究生自拟论文题目或导师与研究生共同商榷确定题目，但需要结合学科、专业的研究方向经过充分调研。

  （三）论文撰写及答辩

  硕士学位论文撰写的基本要求

  1．学位论文题目应以最恰当、最简明、最准确的词语概括论文最重要的内容。

  2．硕士学位论文格式参照《天津财经大学博士、硕士学位论文编写格式规范》

  八、毕业条件与学位授予

  1．本专业硕士研究生应满足以下条件方可毕业：

  （1）修满培养方案要求的学分。

  （2）完成其他必修环节要求。

  （3）完成相关学术活动与科研训练。 5

  （4）通过毕业（学位）论文答辩。其中，选题、写作、学术不端行为检测、外审、答辩等环节应严格按照我校研究生有关规定执行。

  2．本专业授予理学硕士学位。

  九、课程设置与学分分配表

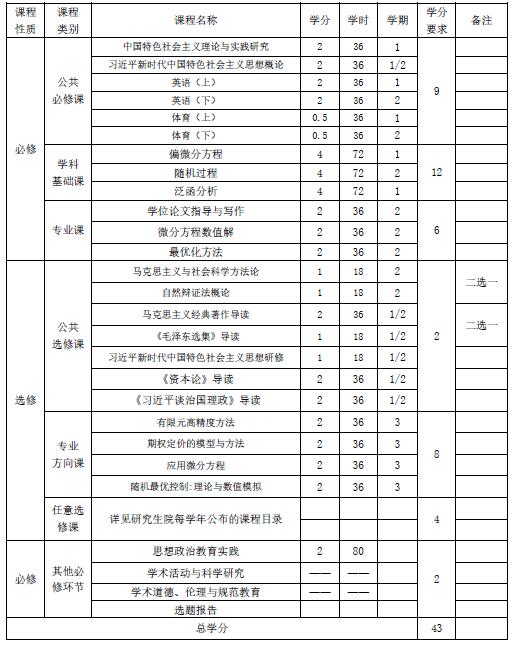
  十、专业阅读书目

  1． 丁同仁， 李承治．常微分方程教程（第二版） [M]． 北京： 高等教育出版社， 2004．

  2． 张芷芬． 常微分方程定性理论[M]． 北京： 科学出版社， 1985．

  3． 范进军． 常微分方程续论[M]． 济南： 山东大学出版社， 2009．

  4． 郑祖庥． 泛函微分方程理论[M]． 合肥： 安徽教育出版社． 1994．

  5． 李森林， 温立志． 泛函微分方程[M]． 长沙： 湖南科技出版社，1987．

  6． 尤秉礼． 常微分方程补充教程[M]． 北京： 人民教育出版社，1981．

  7． Shreve， S．E．， Stochastic Calculus for Finance I： The Binomial Asset Pricing Model， Springer Science & Business Media， 2004．

  8． Shreve， S．E．， Stochastic Calculus for Finance II： Continuous－Time Models， Springer Science & Business Media， 2004．

  9． Evans， L． C． An Introduction to Mathematical Optimal Control Theory， Lecture Notes， University of California， Department of Mathematics， Berkeley， 2005

  10． 余德浩， 汤华中 微分方程数值解法， 科学出版社， 2003 ．

  11． Sethi， S． P． & Thompson， G． L． Optimal Control Theory：Applications to Management Science and Economics， Springer， 2000

  12． 蒋中一． 动态最优化基础． 中国人民大学出版社， 2015．